นักคณิตศาสตร์สามารถคำนวนเส้นรอบวงของโลกได้ตั้งแต่ยุคกรีกโบราณ

การทดลองทางวิทยาศาสตร์ที่ถูกต้องและน่าเหลือเชื่อนี้ มีมาหลายศตวรรษก่อนแล้ว นักคณิตศาสตร์กรีกโบราณ สามารถคำนวนหาเส้นรอบวงของโลกได้อย่างไร

กลางศตวรรษที่20 เราได้ส่งดาวเทียมออกไปสู่อวกาศ โดยมีระยะวงโคจรรอบโลก 40,030กิโลเมตร แต่เมื่อ 2,000 ปีก่อนหน้านี้ในยุคกรีกโบราณที่เมืองอเล็กซานเดรีย ชายคนหนึ่งสามารถคำนวนเส้นรอบวงของโลกได้อย่างแม่นยำโดยการปักไม้ลงบนพื้น ชายคนนั้นคือ เอราทอสเทนีส นักคณิตศาสตร์ยุคกรีกโบราณ และ หัวหน้าบรรณารักษ์หอสมุดอเล็กซานเดรีย เขาได้ยินว่าที่ไซฮีนิ เมืองทางใต้ของอเล็กซานเดรีย ลำแสงอาทิตย์จะส่องลงตรงกลางศีรษะในวันที่กลางวันยาวที่สุดในซีกโลกเหนือ (Summer Solstice)

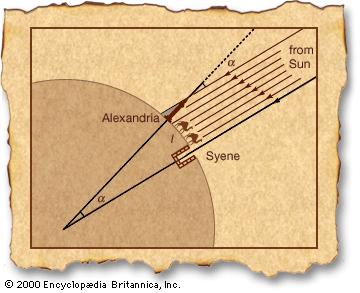
เขาอยากรู้ว่ามันเป็นเช่นนั้นจริงหรือไม่กับเมืองอเล็กซานเดรีย ดังนั้นในวันที่ 21 มิถุนายน เขาได้ปักแท่งไม้ลงพื้นแล้วรอดูว่าเงาของแท่งไม้จะเป็นอย่างไรในตอนเที่ยงของวัน ปรากฎว่ามีเงาทอดออกมาวัดได้ประมาณ 7.2องศา เมื่อแสงส่องมาในมุมเดียวกันวันเดียวกัน แต่แท่งไม้ที่อเล็กซานเดรียมีเงาทอดออกมา ขณะที่แท่งไม้ที่ไซฮีนิไม่มีเงา นั่นแปลว่าผิวโลกจะต้องโค้ง เอราทอสเทนีสอาจรู้แค่นั้น แต่ความคิดเรื่องโลกกลมนี้ถูกพูดถึงกันมากขึ้นในยุคของพิธากอรัสและถูกประเมินโดยอริสโตเติลหลังจากนั้น ถ้าโลกเป็นทรงกลมเอราทอสเทนีสได้ใช้การทดลองนี้ประมาณค่าเส้นรอบวงของโลกทั้งใบได้ เมื่อความต่างของเส้นเงาระหว่างเมืองอเล็กซานเดรียและเมืองไซฮีนิคือ 7.2องศา นั่นหมายถึงเมืองทั้งสองมีมุมที่ห่างกัน 7.2องศาบนโลกทรงกลมที่มีทั้งหมด 360องศา เขาได้จ้างชายคนหนึ่งให้เดินวัดระยะก้าวเดินระหว่างเมืองซานเดรียและเมืองไซฮีนิ และพบว่ามีระยะห่างอยู่ที่ 5,000สเตเดีย หรือประมาณ 800กิโมเมตร เขาได้ทำสูตรคำนวนง่ายๆเพื่อหาเส้นรอบวง โดย 7.2องศาเทียบอัตราส่วนกับ 360องศาได้ค่าเท่ากับ 1/50 ส่วนแล้วนำส่วน 50 มาคูณกับ 800กิโลเมตร จะได้ค่า 40,000กิโลเมตร ด้วยข้อมูลเพียงเท่านี้นักคณิตศาสตร์ใน 2,000 ปีที่แล้วก็สามารถคำนวนหาเส้นรอบวงของโลกได้ โดยใช้แค่แท่งไม้และสมองของเขา

 

 

เรียบเรียง: SignorScience